In middle school, we have learned concepts such as the image of a function and how to draw it , and the image representation of a function .
Generally speaking, for functions
,
If the independent variable is taken as the abscissa and the dependent variable is taken as the ordinate, then a point is determined in the plane rectangular coordinate system . When traverses every value in the domain , the point set
It is called the graph of function ( Figure 1 ) .
Figure 1: [ Animation ]
If the independent variable takes any value within the domain of definition, there is always only one corresponding function value. This kind of function is called a single-valued function. From a geometric point of view, that is: any straight line perpendicular to axis intersects the graph of the function at most at one point.
Figure 2: [ Animation ]
For example, the equation determines a function with as the independent variable and as the dependent variable on the closed interval . It is geometrically a circle with the center at the origin and the radius . It is easy to see that for each , there are two values corresponding to it (see Figure 3) , so is not a single-valued function. However, after additional conditions or , single-valued functions can be obtained respectively
or . [ Animation ]
But the form of the above circle equation in the polar coordinate system is
,
Therefore, it is obviously a single-valued function in the polar coordinate system .
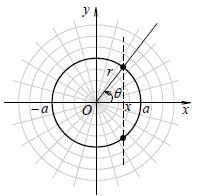
image 3
Note: From now on, unless otherwise stated, functions refer to single-valued functions.

