In high school, we learned the definition of trigonometric functions , the domain of trigonometric functions and the signs of function values , the image properties of sine functions , the image properties of cosine functions , the image properties of tangent functions , and common image transformations of trigonometric functions . As a commonly used basic elementary function, the definition and properties of inverse trigonometric functions will be further given below .
1. Definition of inverse trigonometric function and principal value interval
Generally, the inverse function of a trigonometric function is called an inverse trigonometric function.
Because trigonometric functions
, , , ,
are not monotonic within its domain, so trigonometric functions generally do not have single-valued inverse functions. But in order to get the inverse function of the trigonometric function, we can specifically limit the discussion of the inverse trigonometric function to a certain interval that makes it monotonic . In this way, the trigonometric function is monotonic and single-valued. According to the sufficient conditions for the existence of the inverse function , at this time the trigonometric function The inverse function of the function must exist , and the inverse trigonometric functions of the above trigonometric functions are respectively
, , , ,
Usually we limit the interval that makes the inverse trigonometric function monotonic as:
The above intervals are respectively called the principal value intervals:of the corresponding inverse trigonometric functions .
2. Image properties of commonly used inverse trigonometric functions
(1) Arcsine function , domain , value range :
(Figure 1).
(2) Arc cosine function , domain , value range:
(Figure 2).
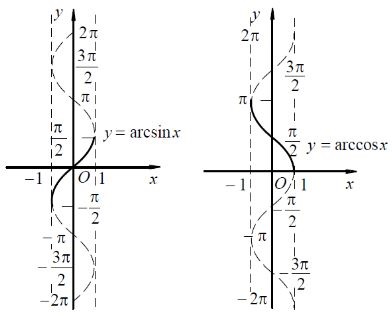
Figure 1:[ Animation ] Figure 2: [ Animation ]
(3) Arctangent function , domain , value range:
(Figure 3).
(4) Inverse cotangent function , domain , value range:
(Figure 4).
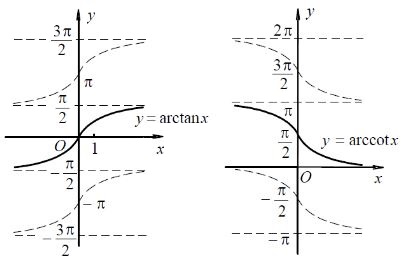
Figure 3:[ Animation ] Figure 4:[ Animation ]

