In order to study the relationship between postage and time for standard ordinary letters (weight not exceeding grams) in a certain country , the following data were obtained:

Try to construct a mathematical model of postage as a function of time . After verifying that this model is " reasonable " , use this model to predict the postage of year .
Solution:(1) First quantify the actual problem and determine the independent variable and dependent variable . Use to represent the time. For the convenience of calculation, let the year be , and use
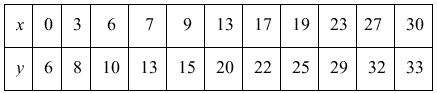
(2) Use statistical chart tools to create scatter plots.

Figure 1 [ Experimental Detailed Explanation ]
[ Scatter Plot and Linear Regression ]
It can be seen from this figure that there is a roughly linear relationship between postage and time, so the functional relationship between and can be set as
, where is an undetermined constant.
(3) Calculate using the linear regression coefficient formula , we get
, .
Thus, the regression straight line is obtained as
.
(4) Adding the above regression line to the scatter plot shows that the linear model fits the scatter plot quite well, indicating that the linear model is reasonable.
(5) Predict the postage in year , that is, the value of at time . Substitute into the above regression line equation to get . It can be predicted that the postage in year will be approximately cents.
In this question, there is a roughly linear relationship between the data pairs of postage and time given in the question. From regression analysis, the straight line is an ideal regression curve. This type of regression problem is also called a linear regression problem. It is the simplest regression analysis. problem, but it has wide practical application value. In addition, many more complex nonlinear regression problems, such as power function, exponential function and logarithmic function regression, can be studied into linear regression problems through appropriate variable replacement.

