It can be seen from the descriptive definition of the limit of the sequence that the changing process of the subscript  and the changing trend of the sequence  both rely on the adjective " infinite " with obvious intuitive ambiguity. From a literary point of view, it is perfect and can arouse people's poetic imagination. Geometric intuition plays a dynamic and active role in the development and creation of mathematics, but intuition alone is unreliable in mathematics. Qualitative descriptions generated by intuition must be transformed into quantitative expressions in mathematical language that transcend realistic prototypes. describe .

　　Observe sequence

The changing trend when  increases infinitely :

　　1. Treat the sequence as a function whose independent variable is a positive integer :

, ( Figure 1 ) .

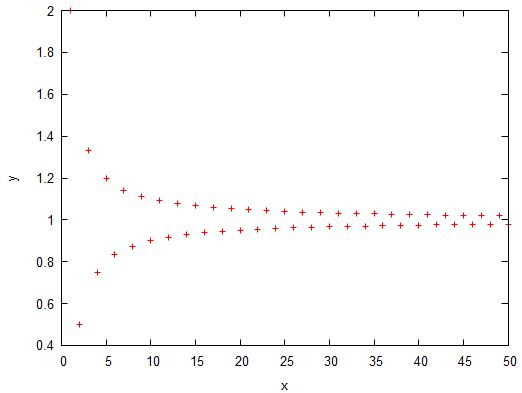
Figure 1：  [ Experiment ]

　　2. Think of as a moving point on the number axis , which takes values sequentially on the number axis.

( Figure 2 ) .

Figure 2：  [ Animation ]

　　It can be seen that this sequence is infinitely close to when increases infinitely . In fact, by

It can be seen that when increases infinitely, the distance between and is infinitely close to . If this trend is described in a certain mathematical language, it is: for any given positive number ( no matter how small it is ) , the total We can find a positive integer such that when , there is always

.

Inspired by this, we can give a strict definition of the limit of a sequence expressed in mathematical language.