在高中的统计一章中，我们学习过回归函数与回归分析的概念，并具体学习了线性回归、回归直线方程及其应用等。下面进一步总结与拓展线性回归相关的问题与应用。

　　在许多实际问题中，人们往往只能通过观测或试验获取反映变量特征的部分经验数据，问题要求我们从这些数据出发来探求隐藏其中的某种模式或趋势。如果这种模式或趋势确实存在，而我们又能找到近似表达这种模式或趋势的曲线

，

那么，我们一方面可以用这个表达式来概括这些数据，另一方面能够以此来预测其它未知处的值。求这样一条拟合指定数据的特殊曲线类型的过程称为回归分析，而该曲线称为回归曲线。

　　有关回归分析的理论要到后续课程(如概率统计课程)中才会涉及，这里，我们仅介绍其中较为简单且又广泛应用的线性回归问题：

　　设有组经验数据

 ，

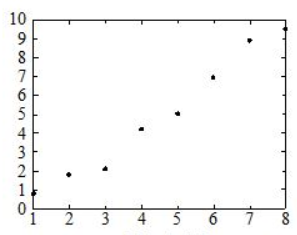
在平面上作出其散点图(见示意图)，如果这些数据之间大致呈线性关系，则可大致确定其线性回归方程：

，

其中，是与上述经验数据有关的特定系数：

，

。

　　注：在高中阶段，我们曾介绍过线性相关系数及其计算，但那时并没有直接给出证明推导。上述待定系数的具体证明推导过程将会在后面学习多元函数极值应用的线性回归问题中给出。