在高中阶段，我们学习了三角函数的定义、三角函数的定义域与函数值的符号、正弦函数的图像性质、余弦函数的图像性质、正切函数的图像性质、三角函数的常用图像变换等。作为常用的基本初等函数，下面再进一步给出反三角函数的定义与性质。

　　1、反三角函数的定义与主值区间

        一般地，三角函数的反函数称为反三角函数。

　　因为三角函数

，，，，

在其定义域内不是单调的，故三角函数一般没有单值的反函数。但为了得到三角函数的反函数，我们可以将反三角函数具体限定在使其单调的某个区间内来讨论，这样，三角函数就单调且单值，根据反函数存在的充分条件，此时三角函数的反函数必存在，并记上述三角函数的反三角函数分别为

，，，，

　　通常我们限定使反三角函数单调的区间为：

上述区间分别称为相应反三角函数的主值区间。

　　2、常用反三角函数的图像性质

　　(1) 反正弦函数，定义域，值域：

 (图1)。

　　(2) 反余弦函数，定义域，值域：

 (图2)。

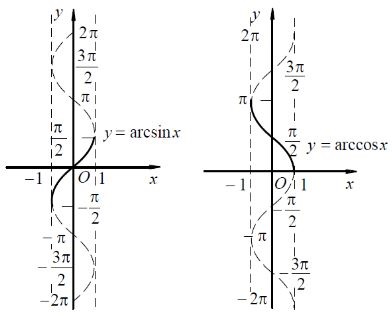
图1 【动画】                      图2 【动画】

　　(3) 反正切函数，定义域，值域：

 (图3)。

　　(4) 反余切函数，定义域，值域：

 (图4)。

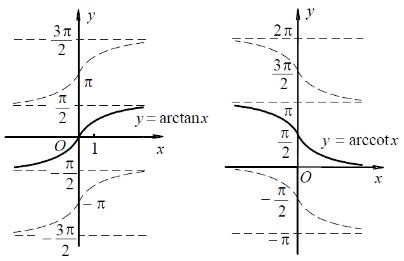
 图3【动画】                         图4【动画】