在日常生活中，我们常常会看到各种曲面。例如，反光镜面、一些建筑物的表面、球面等。与在平面解析几何中把平面曲线看作是动点的轨迹类似，在空间解析几何中，曲面也可看作是具有某种性质的动点的轨迹。

　　定义1　在空间直角坐标系中，若曲面上任一点坐标都满足方程

，

而不在曲面上的任何点的坐标都不满足该方程，则方程

称为曲面的方程，而曲面就称为该方程的图形(图1)。

图1

　　特别地，可以给出空间直角坐标系的三个坐标面(图2)的方程：

面：；

面：；

面：。

　　考虑到平移和旋转并不改变坐标面的平面属性，易知空间直角坐标系中同一个平面的方程都可以由一个三元一次方程来表示，有关空间平面及其方程的详细讨论将在稍后进行。

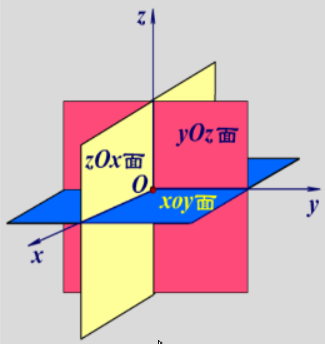
图2

　　建立了空间曲面与其方程的联系后，我们就可以通过研究方程的解析性质来研究曲面的几何性质。

　　空间曲面研究的两个基本问题是：
　　(1) 已知曲面上点所满足的几何条件，建立曲面的方程；

　　例如，求与原点及点的距离之比为的点的全体所构成的曲面的方程(详见本节例2)。

　　(2) 已知曲面方程，研究曲面的几何形状。

　　例如，方程

表示怎样的曲面？(详见本节例3)。