
大学数学《交互查询系统》支持基于大学数学《数字课程系统》与《考研训练系统》数据的考点、题型、试题、试卷的交互查询,从而为用户自主式、个性化的学习考研与训练突破提供巨大的便利,现简要介绍如下:
考点查询:
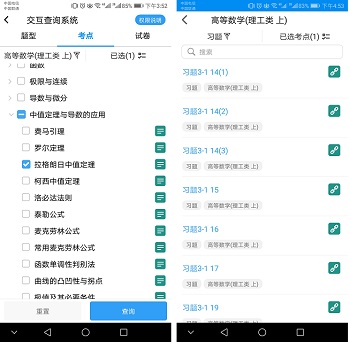
1、考点查看(免费):大学数学考点(850多个知识点)系统全面覆盖教学大纲与考研大纲要求,是作者团队在近20年大学数学教材与教学信息化建设过程中提炼与积累的,考点页面中不仅包含相关定义概念与定理公式,而且包含对相关考点的理解注释、应用方法以及教学动画等,方便用户在同步学习与训练过程中随时查看。
2、考点查询:勾选指定考点,即可查询用到该考点的所有页面数据,包括页面、例题、习题、总习题、典型例题、综合练习与考研真题等,支持用户进一步分类筛选以及打开查询结果中指定的页面内容。这个功能极大地方便用户根据自身的不足,进行考点突破训练,快速提升解题能力。《数字课程系统》和《考研训练系统》中所有的页面均以逻辑推理关系组织了考点(知识点)的交互链接,考点查询功能的实现即赖以此。
3、考点相关题:对查询结果中的每个页面数据,用户可打开数据右侧的“考点相关题”页面,自行设置其中一个或多个的主考点,进一步查询到与所设主考点匹配的相关页面数据,包括页面、例题、习题、总习题、典型例题、综合练习与考研真题等。
题型查询:
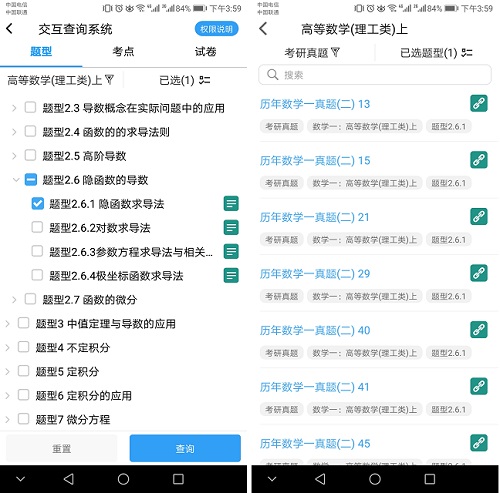
1、题型查看(VIP权限说明,见后):大学数学题型训练系统(数学一:247个题型;数学二:162个题型;数学三:208个题型),全面覆盖教学大纲与考研大纲要求,是作者团队为大学数学《考研训练系统》与《数字课程系统》专门建设的,题型页面中包含相关考点总结、典型例题、综合练习与历年考研真题等,为用户提供了系统的考研题型突破训练。
2、题型查询:勾选指定题型,即可查询与该题型相关的所有页面数据,包括页面、例题、习题、总习题、典型例题、综合练习与考研真题等,支持用户进一步分类筛选以及打开查询结果中指定的页面内容。这个功能极大地方便用户自主式、个性化进行题型突破训练,快速提升解题能力。《数字课程系统》和《考研训练系统》中所有的页面均备注相关题型训练指引,题型查询功能的实现即赖以此。
试卷查询:
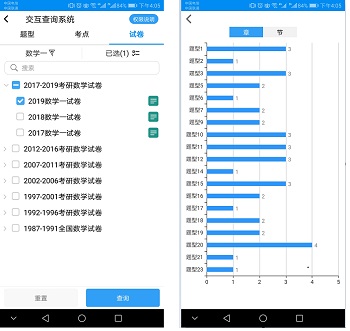
1、考研试卷查看(免费):含1987年-今的历年全国硕士研究生入学统一考试卷,包括数学一、数学二、数学三、数学四以及农林类全真试卷,并为所有考研真题详解过程组织了解题相关的知识点交互链接与相关题型训练指引,为有志考研的用户备考与训练提供极大便利。
2、试卷题型分布:勾选指定试卷(可多选),即可查询与所选试卷相应的题型统计分布柱状图,并可个性化地查询到按章或按节的题型分布图,为用户充分理解与分析历年考研试卷的题型分布提供多角度的定量分析。
3、题型分布详情:在查询试卷得到的题型统计分布柱状图中,每个柱状(图)均为按钮,点击该按钮可进一步弹出与该柱状(图)对应的题型统计分布详情,而对分布详情中的每个页面数据又提供了考点相关题(见考点查询3)的查询与分析。
附:交互查询系统使用权限说明:
1、免费查看:大学数学知识点总结,包含的大学数学各课程850多个知识点总结页面,全面覆盖教学大纲与考研大纲要求,经作者团队在近20年大学数学教材与教学信息化建设过程中提炼总结。考点页面中不仅包含相关定义概念与定理公式,而且包含对相关考点的理解注释、应用方法以及教学动画等。
2、免费查看:历年全国考研全真试卷,包含1987年-今的历年全国硕士研究生数学一、数学二、数学三、数学四以及农林类等统考试卷,并为所有考研真题详解过程组织了解题相关的知识点交互链接与相关题型训练指引,有志考研备考的用户可进一步开通相应课程的VIP模块。
3、交互查询系统支持用户自主式、个性化按题型、考点、试卷查询相关例题、习题、综合练习题与考研全真试题等。对已经开通相应课程的数字课程系统与考研训练系统的用户,查询结果中包含了详解页面的链接。
4、数苑网在法律范围内保留对交互查询系统使用权限的最终解释权。