逻辑联结词：或、且、非，简单命题与复合命题

　　1、逻辑联结词：或、且、非

　　或：用逻辑联结词“或”把命题和命题联结起来，就得到一个新命题，记作“”，读作“或”。

　　且：用逻辑联结词“且”把命题和命题联结起来，就得到一个新命题，记作“”，读作“且”。

　　非：对一个命题否定，就得到一个新命题，记作“”，读作“非”或“的否定”。

　　2、简单命题与复合命题

　　不含逻辑联结词的命题称为简单命题。

　　由简单命题与逻辑联结词构成的命题称为复合命题。
　　一般地，我们研究以下三种复合命题的形式：

或，且，非。

　　3、关于或、且、非的理解

　　(1) 用并集的概念来理解“或”。
　　集合与的并集：

或，

其中的“或”是指与中至少有一个成立，即

且，且，且，

也就是说，逻辑联结词“或”包含“可以兼有”的意思，但并不意味“一定兼有”，这与生活中的“或”的含义不完全相同。
　　从并联电路角度来理解逻辑联结词“或”的含义：如图1所示，若开关的闭合与断开分别对应命题的真与假，则整个电路的接通与断开分别对应命题的真与假。

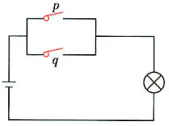
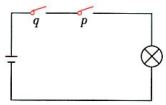
图1　　　　　　　　　　图2

　　(2) 用交集的概念来理解“且”。
　　集合与的交集：

且，

其中的“且”是指与两个条件都要满足的意思。
　　从串联电路角度来理解逻辑联结词“且”的含义：如图2所示，若开关的闭合与断开分别对应命题的真与假，则整个电路的接通与断开分别对应命题的真与假。

　　(3) 用补集的概念来理解“非”。
　　集合的补集：

且

是全集中所有不属于的元素组成的集合，是对的否定，从这个意义上讲，若命题对应集合，则命题非就对应着集合。

　　“非”即否定的意思。一般地，写一个命题的否定，往往需要对正面叙述的词语进行否定。常用的正面词语及其否定整理如下：