在中学阶段，我们先后学习过函数的图像及其画法、函数的图像表示法等概念。

　　一般地，对于函数

，

若取自变量为横坐标，因变量为纵坐标，则在平面直角坐标系中就确定了一个点。当遍取定义域中的每个数值时，点集

称为函数的图形(图1)。

图1 【动画】

　　若自变量在定义域内任取一个数值，对应的函数值总是只有一个，这种函数称为单值函数，从几何上看，即：任意一条垂直于轴的直线与函数的图形最多相交于一点。

图2 【动画】

　　例如，方程在闭区间上确定了一个以为自变量、为因变量的函数，其在几何上即为圆心在原点且半径为的圆。易见，对于每个，都有两个值与之对应(见图3)，因而不是单值函数。但在附加条件或后，可分别得到单值函数

或 。 【动画】

但上述圆方程在极坐标系下的形式为

，

所以，在极坐标系下其显然是单值函数。

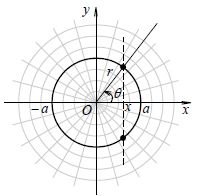
图3

　　注：今后，若无特别声明，函数均指单值函数。