从数列极限的描述性定义可见，下标的变化过程与数列的变化趋势均借助了“无限”这样一个明显带有直观模糊性的形容词。从文学的角度看，不可不谓尽善尽美，并且能激起人们诗一般的想象。几何直观在数学的发展和创造中扮演着充满活力的积极的角色，但在数学中仅凭直观是不可靠的，必须将凭直观产生的定性描述转化为用数学语言表达的超越现实原型的定量描述。

　　观察数列

当无限增大时的变化趋势：

　　1、将数列看作自变量为正整数的函数：

，(图1)。

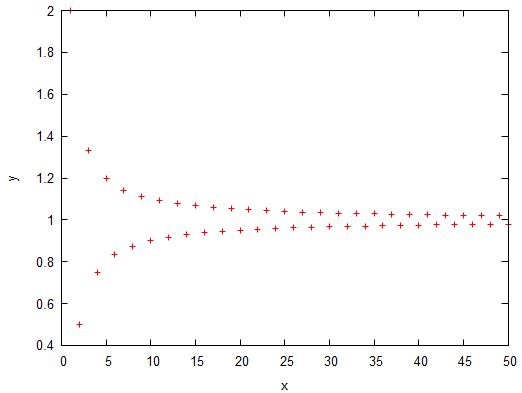
图1  【实验】

　　2、将看作数轴上的动点，它在数轴上依次取值

(图2)。

图2  【动画】

　　由此可见，该数列当无限增大时无限接近于，事实上，由

可见，当无限增大时，与的距离无限接近于，如果以确定的数学语言来描述这种趋势，即有：对于任意给定的正数(不论它多么小)，总可以找到正整数，使得当时，恒有

。

受此启发，我们可以给出用数学语言表达的数列极限的严格定义。